The Spectrum of Learning Analytics
urn:nbn:de:0009-5-45384
Abstract
"Learning Analytics" became a buzzword during the hype surrounding the advent of "big data" MOOCs, however, the concept has been around for over two decades. When the first online courses became available it was used as a tool to increase student success in particular courses, frequently combined with the hope of conducting educational research. In recent years, the same term started to be used on the institutional level to increase retention and decrease time-to-degree. These two applications, within particular courses on the one hand and at the institutional level on the other, are at the two extremes of the spectrum of Learning Analytics – and they frequently appear to be worlds apart. The survey describes affordances, theories and approaches in these two categories.
Keywords: e-learning, learning analytics, data mining, educational data mining, personalization, assessment
Learning Analytics (Duval & Verbert, 2012) arguably started out as Educational Data Mining (EDM) in the mid-nineties (Romero and Ventura, 2007), even though the term "analytics" was not used until later. EDM is technically different from Learning Analytics and Knowledge (LAK) (Siemens & Baker, 2012), but the differences are subtle. EDM has a stronger focus on automation, while LAK has a stronger focus on informing educators and human judgment. EDM follows a reductionist approach, while LAK pursues a holistic approach using frequently different sets of algorithms of varying effectiveness (Papamitsiou & Economides, 2014; Chatti et al., 2014). Overall, LAK is somewhat more "osteopathic" when it comes to treating learning challenges in courses – but the goal is the same: increased learning outcomes. The distinction eventually became less relevant as a much stronger fault line in the field of Learning Analytics emerged (Kortemeyer, 2016a; Kortemeyer, 2017).
While virtually all early efforts focused on individual courses and transactions within those courses (transactional data), the use of the term "Learning Analytics" increasingly moved toward institutional core data (institutional data). Student Information Systems, Registrars, and financial systems were starting to be considered as data sources (EDUCAUSE, 2012). With these new data sources, Learning Analytics moved toward pathways through curricula and towards degrees – with the notable course-level exception of MOOCs (e.g., Kim et al., 2014; Rayyan et al., 2014; Eichhorn & Matkin, 2016). Fig. 1 compares these two ends of the spectrum of Learning Analytics.
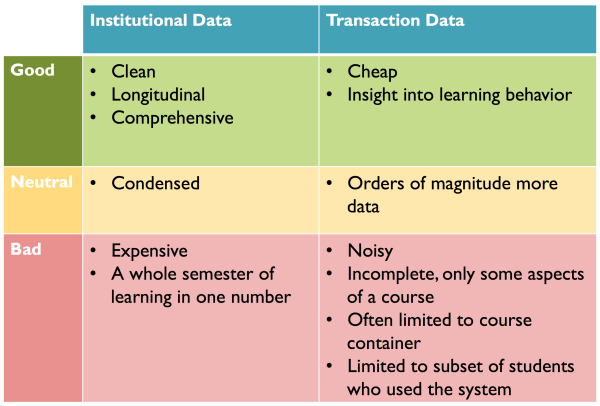
Fig. 1: Institutional versus transactional data as source for Learning Analytics
Institutional data is usually clean, it follows students over their entire tenure at an institution, and it is comprehensive; this is not surprising since degrees depend on the correctness of these data, and at least in the USA, they represent an enormous amount of tuition investment. For better or worse, these data are also condensed, with a whole semester of learning and assessment being compressed into a single data point: the grade. Finally, it is expensive to compile these data, since they are frequently scattered over a variety of disjoint systems and databases from different eras, including legacy systems from the mainframe days - but it is the very combination of these various data sources that often leads to the greatest insights.
Transactional data from courses, on the other hand, are cheap to obtain, since the data is usually a byproduct of running a Course Management System and as such automatically gathered in a single system. Most techniques rely on two data sources within the same system: log files and grade books. The data points track students through their progress within a course and can be used to analyze learning behavior. Instead of boiling down to a single final grade, the online components of a typical course produce three to five orders more magnitude data points per student. However, these data tend to be noisy, as they include undesirable behavior such as copying homework or guessing on answers, as well as more or less random navigational events; these events need to be carefully taken into consideration before drawing conclusions. In most Course Management Systems, the data are limited to a particular course container, and if the use of the system is not mandatory, strong selection effects need to be considered as only a subset of students might use the system.
A common goal of deploying Learning Analytics on an institutional level is increased graduation rate. This ratio of graduating to admitted students is publicly available and an important quality measure of universities in their competition for students; since students (or their parents) typically invest $30-$50k per year in tuition, they consider this figure as a measure of the protection of their investment when deciding where to enroll. Since even state-supported public universities get around 70% of their general (as opposed to project-related) funds from tuition and fees, competition among institutions of higher education is fierce.
As an example of findings from Learning Analytics on an institutional level, a university may be interested trends in Grade Point Averages (GPAs) and their correlation with graduation and persistence. In a recent internal study at Michigan State University of the “Murky Middle” (Venit et al., 2015), it was found that small differences in GPAs between students in early semesters tend to be amplified over time, i.e., upward GPA trends early in a student’s career may be indicative of eventual student success.
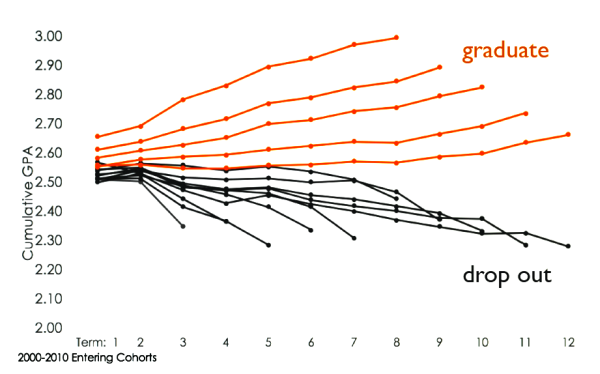
Fig. 2: Divergence of the “Murky Middle” (Venit et al., 2015). Graph courtesy Institutional Studies, Office of Planning and Budgets, Michigan State University.
In particular, it was found that students below a cumulative GPA of 2.55 (with 4.0 being the best grade) after completing one year of college have a high likelihood of not completing their degrees, see Figure 2. This longitudinal diversion of the GPA might be universal, as a similar study at Georgia State University came to the same conclusion, however, with a threshold of first-semester cumulative GPA of 2.4 at their institution. Findings like these lead to increased attention to these early grades and policy decisions to provide more individual coaching and advising to the students who might be in danger of dropping out.
Another interesting phenomenon is the migration of students among majors, particularly in and out of STEM majors (e.g., Maltese & Tai, 2011). For example, at Michigan State University it was found that only 50% of the students initially declaring a STEM major graduate with a STEM degree, while 25% migrate to non-STEM majors and, more alarmingly, 25% never graduate. More than 60% of the students who initially did not declare a major graduate with a non-STEM degree, compared to only 20% who eventually get a STEM degree. Data like these can be used in recruitment to make sure that graduating classes have the desired composition according to departmental capacities, or they can be used in student advising.
US-American universities are concerned about providing equal opportunity for students of all backgrounds (e.g., Murtaugh et al., 1999). Thus, students are tracked by race regarding the number of credits taken per semester and time-to-degree. It is a reason for concern if particular segments of the student population have higher attrition or longer times-to-degree. A recent study at Michigan State University showed that while on the average, white and non-white students take the same number of credits and take equally long to graduate, the achievement spectrum is wider for non-white students, i.e., the tails of the distributions in achievement measures are wider.
The higher education model of Liberal Arts commonly employed in the USA mandates that students take a considerable number of courses outside their majors, where they might have wide leeway in their curricular choices. It is the task of Student Advisors to guide students through their degree requirements, and Learning Analytics are increasingly used to provide new tools for both students and their advisors. Typically, one advisor has to deal with 300 or more students; thus computer-assistance is considered essential.
Tracking the pathways of previous students with different demographics through their curricula, Learning Analytics can make predictions of success for current students in particular future courses. For example, based on historical data, a certain course might be predicted to be "hard" for a particular current student, while another course might be "easier." These selection rules are designed to move students toward graduation most quickly with the highest possible GPA. A common criticism is that these selection rules encourage a curriculum based on grade rather than educational considerations; they might also push student interest into the background of the educational experience.
Course-level Learning Analytics typically puts an emphasis on formative assessment, i.e., the assessment that accompanies the ongoing learning process. Early on, the goal often was the creation of adaptive, personalized, "intelligent" learning environments (EDM philosophy); this turned out to be an uphill battle, as teaching and learning have many "moving parts" (Gašević et al., 2016). Instead of automated systems that attempt to guide learners independent of instructors, today dashboards are providing instructors with Learning Analytics as integrated or pluggable components of Course Management Systems (Verbert et al., 2013). A major goal here is the early identification of students-at-risk, as well as quality control of online materials and Just-In-Time Teaching interventions (Novak, 1999). Also, transactional data deliver valuable research insights for studies on student learning. We illustrate this claim by some examples from introductory physics courses (Kortemeyer, 2014a).
A course is typically composed of a wide variety of educational components: exams, homework, quizzes, labs, materials, as well as possibly attendance and "clicker" questions. Still, we found that up to 87% of this final grade can be predicted by online student behaviors using a combination of different data-mining methods applied to online components of physics courses (Minaei-Bidgoli et al., 2003). As the final grade is largely determined by exam scores, we are essentially considering how well online behavior predicts exam scores.
The most important predictor is the total number of correctly solved online homework problems, followed by the number of tries required to arrive at the correct solution. However, getting a problem correct on the very first attempt is a much weaker predictor, with an impact approximately equal to measures of time-spent-on-task. Apparently, in physics courses, persistence is a better indicator of success than immediate "genius." Participation in online discussions was found to be a weak predictor of success in our physics courses.
A significant problem in physics courses is students falling behind in the materials. As exams are approaching, students might attempt to catch up and read too much material in too short an amount of time. This behavior is frequently called "cramming," but cannot be measured if the course uses traditional textbooks – while instructors may suspect that those do not get read, there is no access log. Learning Analytics of online access data can provide insights into the level to which course structure can discourage this unproductive behavior (Seaton et al. 2014). We analyzed the usage of online course materials in courses at the Massachusetts Institute of Technology and Michigan State University. In courses that were otherwise taught traditionally (weekly end-of-chapter online homework and a small number of midterms), log files show "cramming" before exams, i.e., strong peaks in access frequency of online materials right before exams. Despite weekly homework, students do not regularly access the course materials between exams. Access is also highly selective, as students only read materials immediately relevant for these homework assignments, with extensive portions of the course materials only being accessed by very few students. Attempting to solve problems frequently precedes reading relevant materials.
This unproductive behavior declines when embedding the online homework directly into the materials (as possible in the course management system we are using, LON-CAPA), paired with frequent exams. We found that while in traditional courses, only half of the students read at least half of the materials, in reformed courses, more than 90% of the students do so. The strong access frequency peaks vanish for more distributed smaller peaks. Earlier results already demonstrated that this reformed course structure leads to a more positive attitude toward the course in general and less unproductive problem-solving behavior (Laverty et al., 2012). Combining these findings, more frequent summative assessment (frequent small quizzes instead of few large exams) appears to lead to both qualitatively and quantitatively more efficient learning environments.
The number of tries to solve online homework problems used by students was found to be a predictor of overall course success (Minaei-Bidgoli et al., 2003). Particularly in physics, problems tend to be open-ended free-response, where students type in numbers such as "42.6 Nm" rather than picking one of a limited number of multiple-choice items. This kind of problem, alongside with ranking tasks, while more complex to write, is much more closely coupled with conceptual thinking than simple 1-out-of-N multiple-choice problems (Kortemeyer, 2006).
Instructors are granting anywhere from just one to an infinite number of tries to arrive at the correct solution, and they also employ different reward schemes including reduced credit for using more tries. Unfortunately, these choices can influence student behavior when it comes to random guessing or copying of answers. If students are given a large number of attempts, they frequently do not pay much attention to a particular attempt and enter "random" numbers. Typical patterns include randomly changing the sign, changing the result by factors of two, or by orders of magnitude. For example, we found that more than half of the retries on online homework are submitted within less than one minute of the previous failed attempt when multiple attempts are allowed – hardly enough time for a serious effort on checking answers and derivations (Kortemeyer & Riegler, 2010). Resubmission times are slightly shorter for male than for female students (Kortemeyer, 2009), but in any case below acceptable limits. Granting very few attempts, on the other hand, can lead to students copying answers from others out of desperation. What is a good choice?
We analyzed homework transaction logs from several introductory physics courses for scientists and engineers (Kortemeyer, 2015). These were taught by different instructors who had different policies regarding allowed tries. We found that granting a large number of tries for open-ended free-response online homework is not beneficial. The rate at which students succeed on a given attempt decreases with increasing number of allowed tries, and the rate at which students give up and stop working on problems after a given attempt does not depend on the number of allowed tries. We also found that subsequent attempts to solve online homework were largely independent of each other, i.e., that students frequently did not learn from their mistakes. This finding corresponds to the short resubmission times, as well as unsystematic plug-and-chug strategies that do not allow students to go back through their derivations and fix errors (Kortemeyer, 2016b).
Having a large or even unlimited number of tries appears to lead to less and less desirable problem-solving strategies, as students are not truly taking advantage of these additional chances. Instructors might grant many tries with the intention to allow students to keep working till they master a concept, but we found that running out of tries is a far less likely reason for failure than simply giving up.
The data-driven model, which we developed based on extrapolating trends from the courses with different policies, puts the optimum number at five allowed tries. While students may not be happy with this choice, in reality, it rarely keeps students from eventually solving problems; in a course where five tries were used, the vast majority of students solved almost all homework problems.
Our studies show that homework has a major role in online physics courses, and has a high predictive power. Thus, when developing, deploying, and maintaining online courses, their homework components deserve particular attention, and quality control is essential. Early on, it was shown that Classical Test Theory could successfully be employed to obtain measures of homework item quality (Kortemeyer et al., 2008).
In a summative assessment, e.g., exams, a commonly used tool is Item Response Theory (IRT). We studied if this same tool can be used to evaluate the meaningfulness of online homework (Kortemeyer, 2014b) to enhance Learning Analytics, as well as uncover useful student traits. For example, online homework items that have more desirable item parameters (average difficulty and high discrimination) could receive more weight in subsequent data mining efforts. Due to copying and guessing, as well as multiple allowed tries, this application of IRT is not straightforward.
When using IRT to estimate the learner trait of ability, results obtained from online homework exhibit the expected relation to exam data, but the agreement in absolute terms is moderate. Our earlier, more classical approaches were more successful to gauge student success (Minaei-Bidgoli et al., 2003). When it comes to item parameters, in particular measures of difficulty and discrimination, the latter is less affected by the homework environment than the former.
The agreement of homework and exam data, as well as the quality of item parameters, is not improved by using more complicated models (Gönülateş & Kortemeyer, 2016). This somewhat unexpected finding is true both for traditional higher-order models with a higher number of item parameters, as well as new models we proposed that attempt to model student behavior such as guessing and copying through added student traits.
The effect of considering only the first attempt on homework wears out over the course of the semester as the integrity of student study behavior declines. While in the first quarter of the course, it is one of the strongest indicators, later in the semester, students start working in less and less desirable ways, and first-attempt success becomes more of an indicator of copying solutions than immediate understanding. As found earlier, in the long run, eventually solving a problem is a better indicator of student success than getting problems correct on the very first attempt.
It can easily be argued that Learning Analytics on the institutional level do not analyze learning, but rather work as a tool for optimizing curricular pathways and moving students most efficiently toward the achievement of the product "degree." In these mechanisms, faculty members are frequently treated as interchangeable commodities (Gašević et al., 2016), as historical data on other courses and students are used as the base for selection rules rather than current student-faculty interaction. Learning innovation is discouraged in this framework.
On the other hand, Learning Analytics of transactional data can provide insights into learning behavior. An interesting proposal is the combination of both "worlds" of Learning Analytics, but would this indeed be the "best of both worlds?" A serious concern is student privacy and undue influence: administrators probably should not have access to course-level analytics, as control over the educational experience should remain with the faculty member. On the other hand, faculty members should not have access to the institutional data of a student, as that access may influence their grading decisions. Academic Advisors and the students themselves, however, would benefit from a combination of both "worlds," but currently no efforts in that direction are underway.
Within the two worlds of Learning Analytics, many challenges remain. Learning Analytics on an institutional level can easily lead to one-size-fits-all behavior and neglect of contextual and individual differences. There is a danger of treating education as a commodity toward achieving the final product of a degree; generality is easily achieved but possibly over-emphasized. On the other hand, Learning Analytics on the course level (transactional data), where it arguably has its origins, still appears as an eclectic collection of findings - since we are now dealing with transactions within a particular course, results are strongly context-dependent and may lack generality.
Chatti, M. A.; Lukarov, V.; Thüs, H.; Muslim, A.; Yousef, A. M. F.; Wahid, U.; Schroeder, U. (2014): Learning Analytics: Challenges and future research directions. In: eleed, Iss. 10, 2014. urn:nbn:de:0009-5-40350 (last check 2017-06-24).
Duval, E.; Verbert, K. (2012): Learning analytics. In: eleed, Iss. 8, 2012. urn:nbn:de:0009-5-33367. (last check 2017-06-24)
EDUCAUSE Learning Initiative Learning Analytics Resources. https://net.educause.edu/section_params/conf/eli124/LearningAnalyticsResources.pdf (last check 2017-06-24)
Eichhorn, S.; Matkin, G. W. (2016): Massive Open Online Courses, Big Data, and Education Research. In: New Directions for Institutional Research, Vol. 167, 2015, pp. 27-40. doi:10.1002/ir.20152 (last check 2017-06-24)
Gašević, D.; Dawson, S.; Rogers, T.; Gašević, D. (2016): Learning analytics should not promote one size fits all: The effects of instructional conditions in predicting academic success. In: The Internet and Higher Education, Vol. 28, 2016, pp. 68-84. doi:10.1016/j.iheduc.2015.10.002 (last check 2017-06-24)
Gönülateş, E.; Kortemeyer, G. (2016): Modeling Unproductive Behavior in Online Homework in Terms of Latent Student Traits: An Approach Based on Item Response Theory. In: Journal of Science Education and Technology, 2016, pp. 1-12.
Kim, J.; Guo, P. J.; Seaton, D. T.; Mitros, P.; Gajos, K. Z.; Miller, R. C. (2014): Understanding in-video dropouts and interaction peaks in online lecture videos. In: Proceedings of the First ACM Conference on Learning @ Scale Conference - L@S '14. 2014, pp. 31-40. doi:10.1145/2556325.2566237 (last check 2017-06-24)
Kortemeyer, G. (2006): An analysis of asynchronous online homework discussions in introductory physics courses. In: Am. J. Phys. American Journal of Physics, Vol. 74, 2006, pp. 526. doi:10.1119/1.2186684 (last check 2017-06-24)
Kortemeyer, G.; Kashy, E.; Benenson, W.; Bauer, W. (2008): Experiences using the open-source learning content management and assessment system LON-CAPA in introductory physics courses. In: Am. J. Phys. American Journal of Physics, Vol 76, 2008, 4, pp. 438. doi:10.1119/1.2835046 (last check 2017-06-24)
Kortemeyer, G. (2009): Gender differences in the use of an online homework system in an introductory physics course. In: Physical Review Special Topics - Physics Education Research Phys. Rev. ST Phys. Educ. Res., Vol. 5, 2009, 1. doi:10.1103/physrevstper.5.010107 (last check 2017-06-24)
Kortemeyer, G.; Riegler, P. (2010): Large-Scale E-Assessments, Prüfungsvor-und-nachbereitung: Erfahrungen aus den USA und aus Deutschland. In: Zeitschrift für E-learning-Lernkultur und Bildungstechnologie, Themenheft E-Assessment, Vol. 8, 2010, pp. 22.
Kortemeyer, G. (2014a): Over two decades of blended and online physics courses at Michigan State University. In: eleed, Iss. 10, 2014. urn:nbn:de:0009-5-40115 (last check 2017-06-24)
Kortemeyer, G. (2014b): Extending item response theory to online homework. In: Phys. Rev. ST Phys. Educ. Res., Vol. 10, 2014, 1. doi:10.1103/physrevstper.10.010118 (last check 2017-06-24)
Kortemeyer, G. (2015). An empirical study of the effect of granting multiple tries for online homework. In: Am. J. Phys. American Journal of Physics, Vol. 83, 2015, 7, pp. 646-653. doi:10.1119/1.4922256 (last check 2017-06-24)
Kortemeyer, G. (2016a): The Two Worlds of Learning Analytics. In: Educause Review Online, 2016-03-07. https://er.educause.edu/blogs/2016/3/the-two-worlds-of-learning-analytics (last check 2017-06-24)
Kortemeyer, G. (2016b): The Losing Battle Against Plug-and-Chug. In: The Physics Teacher Phys. Teach., Vol. 54, 2016, 1, pp. 14-17. doi:10.1119/1.4937964
Kortemeyer, G. (2017): Die zwei Welten von Learning Analytics. Presentation, CampusSource Tagung 2017, http://www.campussource.de/events/e1703hagen/docs/Kortemeyer_Analytics.pdf (last check 2017-06-24)
Laverty, J. T.; Bauer, W.; Kortemeyer, G.; Westfall, G. (2012): Want to Reduce Guessing and Cheating While Making Students Happier? Give More Exams! In: The Physics Teacher Phys. Teach., Vol. 50, 2012, 9, pp. 540. doi:10.1119/1.4767487 (lastc check 2017-06-24)
Maltese, A. V.; Tai, R. H. (2011): Pipeline persistence: Examining the association of educational experiences with earned degrees in STEM among US students. In: Science Education, Vol. 95, 2011, 5, pp. 877-907.
Minaei-Bidgoli, B.; Kashy, D.; Kortemeyer, G.; Punch, W. (n.d.): Predicting student performance: An application of data mining methods with an educational web-based system. In: 33rd Annual Frontiers in Education, 2003. FIE 2003. doi:10.1109/fie.2003.1263284 (last check 2017-06-24)
Murtaugh, P. A.; Burns, L. D.; Schuster, J. (1999): Predicting the retention of university students. In: Research in higher education, Vol. 40, 1999, 3, pp. 355-371.
Novak, G. M. (1999): Just-in-time teaching: Blending active learning with web technology. Prentice Hall, Upper Saddle River, NJ , 1999.
Papamitsiou, Z. K.: Economides, A. A. (2014): Learning analytics and educational data mining in practice: A systematic literature review of empirical evidence. In: Educational Technology & Society, Vol. 17, 2014, 4, pp. 49-64.
Rayyan, S.; Seaton, D. T.; Belcher, J.; Pritchard, D. E.; Chuang, I. (2014): Participation and Performance in 8.02x Electricity and Magnetism: The First Physics MOOC from MITx. 2013. In: Physics Education Research Conference Proceedings, 2014, pp. 289-292. doi:10.1119/perc.2013.pr.060 (last check 2017-06-24)
Romero, C.; Ventura, S. (2007): Educational data mining: A survey from 1995 to 2005. In: Expert Systems with Applications, Vol. 33, 2007, 1, pp. 135-146. doi:10.1016/j.eswa.2006.04.005 (last check 2017-06-24)
Seaton, D. T.; Bergner, Y.; Kortemeyer, G.; Rayyan, S.; Chuang, I.; Pritchard, D. E. (2014): The Impact of Course Structure on eText Use in Large-Lecture Introductory-Physics Courses. In: 2013 Physics Education Research Conference Proceedings, 2014, pp. 333-336. doi:10.1119/perc.2013.pr.071 (last check 2017-06-24)
Siemens, G.; Baker, R. S. (2012): Learning analytics and educational data mining. In: Proceedings of the 2nd International Conference on Learning Analytics and Knowledge - LAK '12. 2012, pp. 252-254. doi:10.1145/2330601.2330661 (last check 2017-06-24)
Verbert, K.; Duval, E.; Klerkx, J.; Govaerts, S.; Santos, J. L. (2013): Learning Analytics Dashboard Applications. In: American Behavioral Scientist, Vol. 57, 2013, 10, pp. 1500-1509. doi:10.1177/0002764213479363 (last check 2017-06-24)
Venit, E., et al. (2015): The Murky Middle Project. Advisory Board Company, Washington, DC, 2015.